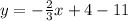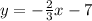Question

write the equation in slope-intercept form of the line that passes through (6,-11) and is parallel to the graph of y=-2/3x+12

Answer 1

`y = -(2)/(3)x - 7`

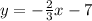
Explanation:

Given

`Point = (6,-11)`

`Equation: y = -(2)/(3)x + 12`

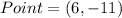
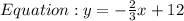
Required

Determine the equation of the point

First, we need to determine the slope of the point.

Since the point is parallel to the given equation, then they have the same slope (m).

The general form of an equation is:

`y = mx + b`

Where

`m = slope`

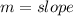
By comparison:

`m = -(2)/(3)`

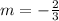
The equation of the point in slope intercept point is:

`y -y_1 = m(x-x_1)`

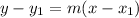
Where

`m = -(2)/(3)`

`(x_1,y_1) = (6,-11)`

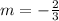
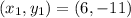
Substitute these values in the equation:

`y - (-11) = -(2)/(3)(x - 6)`

`y +11 = -(2)/(3)(x - 6)`

`y +11 = -(2)/(3)x + (2)/(3)*6`

`y +11 = -(2)/(3)x + 4`

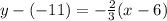
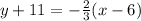
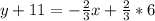
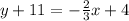
Subtract 11 from both sides

`y = -(2)/(3)x + 4-11`

`y = -(2)/(3)x - 7`