Question

Are the angles 117 in degrees and 477 in degrees coterminal?

Answer 1

You are given 117°.

To find angles that are coterminal with 117°, we do the following:

117° + 360° = 477°

117° - 360° = 243°

As you can see, when we added 117° to 360°, we got 477°.

To answer your question, YES.

You now know that 117° and 477° are coterminal angles.

Keep in mind that 477° is not the only coterminal angle to 117°.

Answer 2

Yes, they are coterminal.

Explanation:

Coterminal angles are angles that are in multiples of -360 degrees or +360 degrees away from the initial angle.

Therefore, the easiest way to check if an angle is coterminal is set up an equation.

`x + 117 = 477\\\\360 + 117 = 477\\\\477 = 477 \ \checkmark`

We get a true statement, which means that 117 is a coterminal angle of 477 and 477 is a coterminal angle of 117.

We can also determine the value in radians.

`\displaystyle117 * (\pi)/(180)\\\\(117\pi)/(180) = (13\pi)/(20)`

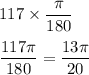
117° in radians is
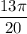`\displaystyle(13\pi)/(20)`. Coterminal angles for radians are multiples of
`2\pi`, either negative or positive.

However, we also need to determine the value of 477 in radians too.

`\displaystyle477*(\pi)/(180)\\\\(477\pi)/(180) = (53\pi)/(20)`

So, if we add
`2\pi` to
`(13\pi)/(20)`:

`\displaystyle(13\pi)/(20) + 2\pi\\\\(13\pi)/(20) + (40\pi)/(20) = (53\pi)/(20)`

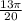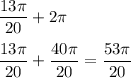
Therefore, even in radians, 477° is an angle coterminal to 117°.