Question

Use root test to determine the series is convergent/divergent or inconclusive

Answer 1

You can first condense the series to make it simpler to study. If n is odd, then n = 2k - 1, and if n is even, then n = 2k for some k ≥ 1. So for each k, you can pair up the k-th terms of the odd- and even-indexed series.

odd:

`\frac1{3^{\frac{n+3}2}}=\frac1{3^(k+1)}`

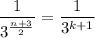
even:

`\frac1{3^(\frac n2)}=\frac1{3^k}`

So the series can be re-indexed as

`\displaystyle\sum_(n=1)^\infty a_n=\sum_(k=1)^\infty a_k=\sum_(k=1)^\infty \left(\frac1{3^(k+1)}+\frac1{3^k}\right)=\sum_(k=1)^\infty\frac4{3^(k+1)}`

By the root test, the series converges, since

`\displaystyle\lim_(k\to\infty)\sqrt[k]{\left|\frac4{3^(k+1)}\right|}=\frac13\lim_(k\to\infty)\left(\frac43\right)^(\frac1k)=\frac13<1`