Question

Find the area of a right isosceles triangle with hypotenuse 10\sqrt{2}10
2 units

Answer 1

A = 50 square units

Explanation:

Right Triangles

A right triangle is identified because it has one internal angle of 90°.

The longest side is called hypotenuse and the other two sides are called legs. Being c the hypotenuse and a and b the legs, the Pythagora's theorem relates the with the equation:

`c^2=a^2+b^2`

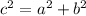
If the triangle is also isosceles, then both legs have the same measure or a=b:

`c^2=a^2+a^2=2a^2`

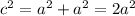
Since we know the hypotenuse has a measure of 10\sqrt{2}:

`(10√(2))^2=2a^2`

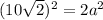
Operating:

`100*2=2a^2`

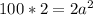
Dividing by 2:

`a^2=100~~\Rightarrow a=√(100)`

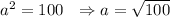
a = 10 units

The area of the triangle is:

`\displaystyle A=(a.b)/(2)`

`\displaystyle A=(10*10)/(2)`

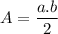
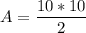
A = 50 square units