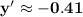Answer:
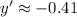
Explanation:
Implicit Derivatives
When it's not possible to express one variable as an explicit function of the other, we use implicit derivatives and solve for y'.
Find y' in the equation given below:
xe^y - 4y = 3x - 14 + 2e^2
Taking derivatives with respect to x, recalling y'=dy/dx, and dx/dx=1:
(xe^y)' - (4y)' = (3x)' - (14 + 2e^2 )'
Using the product rule for the first derivative, and simple rules for the rest:
e^y + xe^yy' - 4y' = 3 - 0
Recall the derivative of a constant is zero.
Group terms with y' in the left side and the rest in the right side:
xe^yy' - 4y' = 3 - e^y
Factoring y':
y'(xe^y - 4) = 3 - e^y
Solving:
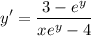
Evaluating for x=2, y=2:
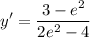
Calculating: