Question

The vertices of a triangle are A(-2, 1), B(2, 2) and C(6, - 2).

Find the equation of the altitude of AD drawn from A to BC.​

Answer 1

The equation of altitude AD drawn from A to BC will be:

`y=x+3`

Explanation:

Let m₁ and m₂ be the slope of line AD and BC respectively.

Now, AD⊥BC

​∴ m₁ × m₂ = -1

be the slope of line AD and BC respectively.

⇒ m₁ = -1/m₂ → (A)

Finding the slope of BC using points

B(2, 2)

C(6, - 2)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(2,\:2\right),\:\left(x_2,\:y_2\right)=\left(6,\:-2\right)`

`m_(2) =(-2-2)/(6-2)`

`m_(2) =-1`

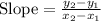
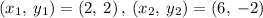
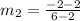
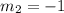
On substituting the value of m₂ in equation (A)

m₁ = -1/m₂

= -1/(-1)

= 1

We know that the point-slope form of the line equation is

`y-y_1=m\left(x-x_1\right)`

∴ Equation of altitude AD passing through A(-2, 1) with slope 1 will be

`y-1=1\cdot \left(x-\left(-2\right)\right)`

`y-1=x+2`

`y=x+3`

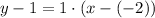
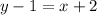
Therefore, the equation of altitude AD drawn from A to BC will be:

`y=x+3`