Answer:
Value of a =3
Value of b =5
Explanation:
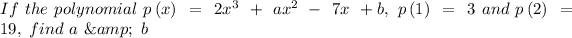
We are given p(1)=3 and p(2)=19
Putting x =1 to find p(1)
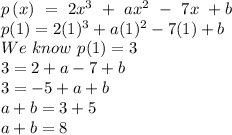
Now putting x=2 as p(2)=19
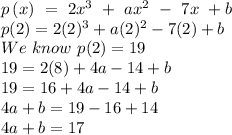
Solving these equations to find values of a and b
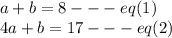
Subtract both equations
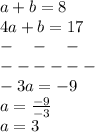
So, value of a =3
Now finding value of b bu putting value of a in equation 1
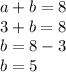
So, Value of b =5