Question

Prove the sum of two rational numbers is rational where a, b, c, and d are integers and b and d cannot be zero. Fill in the missing step in the proof.

Answer 1

We conclude that the sum of two rational numbers is rational.

Hence, the fraction will be a rational number. i.e.

• 
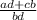  `(ad+cb)/(bd)` ∵ b≠0, d≠0, so bd≠0

Explanation:

Let a, b, c, and d are integers.

Let a/b and c/d are two rational numbers and b≠0, d≠0

Proving that the sum of two rational numbers is rational.

`(a)/(b)+(c)/(d)`

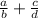
As the least common multiplier of b, d: bd

Adjusting fractions based on the LCM

`(a)/(b)+(c)/(d)=(ad)/(bd)+(cb)/(db)`

`\mathrm{Since\:the\:denominators\:are\:equal,\:combine\:the\:fractions}:\quad (a)/(c)\pm (b)/(c)=(a\pm \:b)/(c)`

`=(ad+cb)/(bd)`

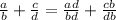
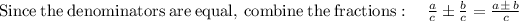
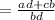
As b≠0, d≠0, so bd≠0

Therefore, we conclude that the sum of two rational numbers is rational.

Hence, the fraction will be a rational number. i.e.

• 
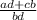  `(ad+cb)/(bd)` ∵ b≠0, d≠0, so bd≠0