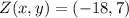Question

Coordinates of Z if Y is the midpoint of XZ, X(10,9) and Y(-4,8)

Answer 1

`Z(x,y) = (-18,7)`

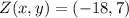
Explanation:

Given

`X = (10,9)`

`Y = (-4,8)`

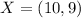
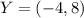
Required

Determine the coordinates of Z

From the question, we understand that Y is the midpoint

And the midpoint is calculated as:

`(x,y) = ((x_1+x_2)/(2),(y_1+y_2)/(2))`

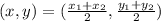
In this case:

`Y(x,y) = (-4,8)`

`X(x_1,y_1) = (10,9)`

`Z = (x_2,y_2)`

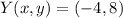
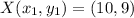
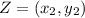
So: This gives

`(x,y) = ((x_1+x_2)/(2),(y_1+y_2)/(2))`

`(-4,8) = ((10+x_2)/(2),(9+y_2)/(2))`

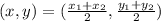
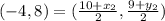
Multiply through by 2

`(-8,16) = (10 + x_2,9+y_2)`

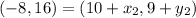
By comparison:

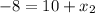`-8 = 10 + x_2` and
`16 = 9 + y_2`

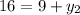
Solving for x2

`-8 = 10 + x_2`

`-8 - 10 = x_2`

`-18 = x_2`

`x_2 = -18`

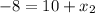
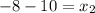
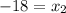
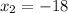
Solving for y2

`16 = 9 + y_2`

`16 - 9 = y_2`

`7 = y_2`

`y_2 = 7`

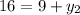
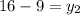
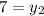
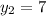
Hence, the coordinates of Z is:

`Z(x,y) = (-18,7)`