Question

What is the slope of each side of the triangle? the sides are A(-2,4) B(-1,1) C(2,3)

Answer 1

The slopes of three sides of triangle are as follows:

AB = -3

BC = 2/3

AC = -1/4

Explanation:

The slope is denoted by m and is calculated using the formula

`m = (y_2-y_1)/(x_2-x_1)`

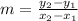
The given vertices are:

A(-2,4) B(-1,1) C(2,3)

The sides will be:

AB, BC, AC

Let m1 be the slope of AB

Let m2 be the slope of BC

Let m3 be the slope of AC

Now

`Slope\ of\ AB = m_1 = (1-4)/(-1+2) = (-3)/(1) = -3\\Slope\ of\ BC = m_2 = (3-1)/(2+1) = (2)/(3)\\Slope\ of\ AC = m_2 = (3-4)/(2+2) = (-1)/(4) = -(1)/(4)`

Hence,

The slopes of three sides of triangle are as follows:

AB = -3

BC = 2/3

AC = -1/4