Question

A beam contains 4.9 × 108 doubly charged positive ions per cubic centimeter, all of which are moving north with a speed of 4.6 × 105 m/s. What is (a) the magnitude of the current density and (b) direction of the current density (c) what additional quantity do you need to calculate the total current i in this ion beam?

Answer 1

`72.12\ \text{A/m}^2`

south

cross sectional area of the beam

Step-by-step explanation:

v = Velocity of ions =
`4.6* 10^5\ \text{m/s}`

Number of ions per
`\text{cm}^3` =
`4.9* 10^8`

Charge density would be the product of number of ions per
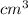`cm^3` and the charge of electrons multiplied by 2 as they are doubly charged.

`\rho_q=4.9* 10^8* 10^6* 2* 1.6* 10^(-19)\\\Rightarrow \rho_q=0.0001568\ \text{C/m}^3`

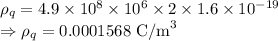
Current density is given by

`J=\rho_qv\\\Rightarrow J=0.0001568* 4.6* 10^5\\\Rightarrow J=72.12\ \text{A/m}^2`

The current density is
`72.12\ \text{A/m}^2`

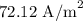
The direction of the current density is opposite to the movement of the charged particle. The particles are moving north so the direction of current density will be to the south.

Current is given by

`I=JA`

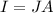
where A is the cross sectional area of the beam .

So the cross sectional area of the beam is required to determine the total current in this ion beam.