Answer:
The diameter of a circle with the equation is 16.
Explanation:
Given the equation
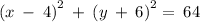
We know that the circle equation with radius 'r', centered at (a, b)
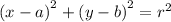
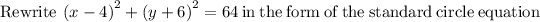
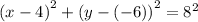
Here,
radius = r = 8
center = (4, -6)
Hence, the radius of the circle is: r = 8
we know that
diameter = 2r
= 2(8)
= 16
Therefore, the diameter of a circle with the equation is 16.