Question

Solve the system of equations.



−2x+5y =−35
7x+2y =25

Answer 1

The equations have one solution at (5, -5).

Explanation:

We are given a system of equations:

`\displaystyle{\left \{ {{-2x+5y=-35} \atop {7x+2y=25}} \right.}`

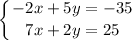
This system of equations can be solved in three different ways:

1. Graphing the equations (method used)
2. Substituting values into the equations
3. Eliminating variables from the equations

Graphing the Equations

We need to solve each equation and place it in slope-intercept form first. Slope-intercept form is
`\text{y = mx + b}`.

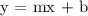Equation 1 is
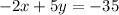`-2x+5y = -35`. We need to isolate y.

`\displaystyle{-2x + 5y = -35}\\\\5y = 2x - 35\\\\(5y)/(5) = (2x - 35)/(5)\\\\y = (2)/(5)x - 7`

Equation 1 is now
`y=(2)/(5)x-7`.

Equation 2 also needs y to be isolated.

`\displaystyle{7x+2y=25}\\\\2y=-7x+25\\\\(2y)/(2)=(-7x+25)/(2)\\\\y = -(7)/(2)x + (25)/(2)`

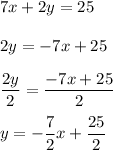
Equation 2 is now
`y=-(7)/(2)x+(25)/(2)`.

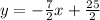Now, we can graph both of these using a data table and plotting points on the graph. If the two lines intersect at a point, this is a solution for the system of equations.

The table below has unsolved y-values - we need to insert the value of x and solve for y and input these values in the table.

`\begin{array} \cline{1-2} \textbf{x} & \textbf{y} \\ \cline{1-2} 0 & a \\ \cline{1-2} 1 & b \\ \cline{1-2} 2 & c \\ \cline{1-2} 3 & d \\ \cline{1-2} 4 & e \\ \cline{1-2} 5 & f \\ \cline{1-2} \end{array}`

`\bullet \ \text{For x = 0,}`

`\displaystyle{y = (2)/(5)(0) - 7}\\\\y = 0 - 7\\\\y = -7`

`\bullet \ \text{For x = 1,}`

`\displaystyle{y=(2)/(5)(1)-7}\\\\y=(2)/(5)-7\\\\y = -(33)/(5)`

`\bullet \ \text{For x = 2,}`

`\displaystyle{y=(2)/(5)(2)-7}\\\\y = (4)/(5)-7\\\\y = -(31)/(5)`

`\bullet \ \text{For x = 3,}`

`\displaystyle{y=(2)/(5)(3)-7}\\\\y= (6)/(5)-7\\\\y=-(29)/(5)`

`\bullet \ \text{For x = 4,}`

`\displaystyle{y=(2)/(5)(4)-7}\\\\y = (8)/(5)-7\\\\y=-(27)/(5)`

`\bullet \ \text{For x = 5,}`

`\displaystyle{y=(2)/(5)(5)-7}\\\\y=2-7\\\\y=-5`

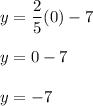
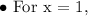
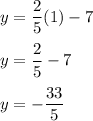
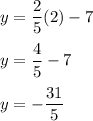
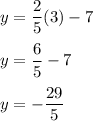
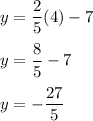
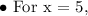
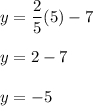
Now, we can place these values in our table.

`\begin{array} \cline{1-2} \textbf{x} & \textbf{y} \\ \cline{1-2} 0 & -7 \\ \cline{1-2} 1 & -33/5 \\ \cline{1-2} 2 & -31/5 \\ \cline{1-2} 3 & -29/5 \\ \cline{1-2} 4 & -27/5 \\ \cline{1-2} 5 & -5 \\ \cline{1-2} \end{array}`

As we can see in our table, the rate of decrease is
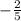`-(2)/(5)`. In case we need to determine more values, we can easily either replace x with a new value in the equation or just subtract
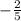`-(2)/(5)` from the previous value.

For Equation 2, we need to use the same process. Equation 2 has been resolved to be
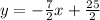`y=-(7)/(2)x+(25)/(2)`. Therefore, we just use the same process as before to solve for the values.

`\bullet \ \text{For x = 0,}`

`\displaystyle{y=-(7)/(2)(0)+(25)/(2)}\\\\y = 0 + (25)/(2)\\\\y = (25)/(2)`

`\bullet \ \text{For x = 1,}`

`\displaystyle{y=-(7)/(2)(1)+(25)/(2)}\\\\y = -(7)/(2) + (25)/(2)\\\\y = 9`

`\bullet \ \text{For x = 2,}`

`\displaystyle{y=-(7)/(2)(2)+(25)/(2)}\\\\y = -7+(25)/(2)\\\\y = (11)/(2)`

`\bullet \ \text{For x = 3,}`

`\displaystyle{y=-(7)/(2)(3)+(25)/(2)}\\\\y = -(21)/(2)+(25)/(2)\\\\y = 2`

`\bullet \ \text{For x = 4,}`

`\displaystyle{y=-(7)/(2)(4)+(25)/(2)}\\\\y=-14+(25)/(2)\\\\y = -(3)/(2)`

`\bullet \ \text{For x = 5,}`

`\displaystyle{y=-(7)/(2)(5)+(25)/(2)}\\\\y = -(35)/(2)+(25)/(2)\\\\y = -5`

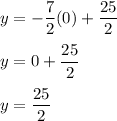
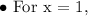
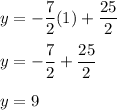
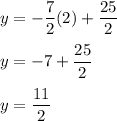
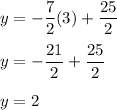
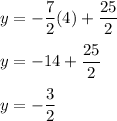
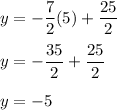
And now, we place these values into the table.

`\begin{array} \cline{1-2} \textbf{x} & \textbf{y} \\ \cline{1-2} 0 & 25/2 \\ \cline{1-2} 1 & 9 \\ \cline{1-2} 2 & 11/2 \\ \cline{1-2} 3 & 2 \\ \cline{1-2} 4 & -3/2 \\ \cline{1-2} 5 & -5 \\ \cline{1-2} \end{array}`

When we compare our two tables, we can see that we have one similarity - the points are the same at x = 5.

Equation 1 Equation 2

`\begin{array}c \cline{1-2} \textbf{x} & \textbf{y} \\ \cline{1-2} 0 & -7 \\ \cline{1-2} 1 & -33/5 \\ \cline{1-2} 2 & -31/5 \\ \cline{1-2} 3 & -29/5 \\ \cline{1-2} 4 & -27/5 \\ \cline{1-2} 5 & -5 \\ \cline{1-2} \end{array}`
`\begin{array}c \cline{1-2} \textbf{x} & \textbf{y} \\ \cline{1-2} 0 & 25/2 \\ \cline{1-2} 1 & 9 \\ \cline{1-2} 2 & 11/2 \\ \cline{1-2} 3 & 2 \\ \cline{1-2} 4 & -3/2 \\ \cline{1-2} 5 & -5 \\ \cline{1-2} \end{array}`

Therefore, using this data, we have one solution at (5, -5).