Question

Rewrite the following expression performing the subtraction.

(5c² - 3c + 9) - (2c²+ 8c - 3)
a) What did you need to distribute to the second polynomial to rewrite?

Perform subtraction. Then, answer:

b) How many terms? in the simplified expression

c) What is the leading coefficient of the simplified expression?

d) What is the degree of the simplified expression?

Answer 1

a)
`3c^2-11c+12`

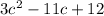
b) 3 terms in simplified expression

c) 3 is leading coefficient

d) 2 is the degree of simplified expression

Explanation:

We need to perform subtraction of
`(5c^2 - 3c + 9) - (2c^2+ 8c - 3)`

a) What did you need to distribute to the second polynomial to rewrite?

We need to multiply - sign with the terms inside the bracket.

Perform subtraction. Then, answer:

`(5c^2 - 3c + 9) - (2c^2+ 8c - 3)\\=5c^2 - 3c + 9 - 2c^2- 8c +3\\Combining \ like \ terms\\=5c^2-2c^2-3c-8c+9+3\\=3c^2-11c+12`

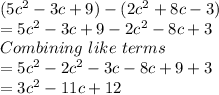
b) How many terms in the simplified expression?

There are 3 terms in the simplified solution
`3c^2-11c+12`

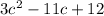
c) What is the leading coefficient of the simplified expression?

The leading coefficient is the coefficient with highest degree. The highest degree is 2 so, leading coefficient is 3

d) What is the degree of the simplified expression?

The highest degree is considered as the degree of simplified expression. In our case
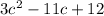`3c^2-11c+12` the highest degree is 2