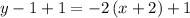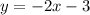Question

5. What is the equation of a line that is perpendicular to -x + 2y = 4 and passes through the point (-2,1)?

a.
Write the equation -x + 2y = 4 in slope-intercept form
b. Identify the slope of the line represented in part a.
C.
What is the slope of the line perpendicular to the line in steps a and b?
d. Write the equation of the perpendicular line in slope-intercept form.

Answer 1

Please check the explanation.

Explanation:

Given the equation

`-x + 2y = 4`

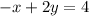
a) writing the equation in the slope-intercept form

We know that the slope-intercept form of the equation of the line is

`y=mx+b`

where m is the slope of the line

so writing the equation in the slope-intercept form

`-x + 2y = 4`

`2y=4+x`

`y=(1)/(2)x+2`

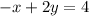
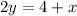
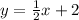
b) Identify the slope of the line represented in part a

As the equation in slope-intercept form is

`y=(1)/(2)x+2`

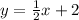
Here,

m = slope = 1/2 ∵
`y=mx+b`

c) What is the slope of the line perpendicular to the line in steps a and b

As we know that the slope of the perpendicular line is basically the negative reciprocal of the slope of the line, so

As the slope = 1/2

So the slope of the perpendicular line will be: -2

d. Write the equation of the perpendicular line in slope-intercept form.

Therefore, the point-slope form of the equation of the perpendicular line that goes through (-2,1) is:

`y-y_1=m\left(x-x_1\right)`

substituting the values m = -2 and the point (-2,1)

`\:y-1=-2\left(x-\left(-2\right)\right)`

`y-1=-2\left(x+2\right)`

Add 1 to both sides

`y-1+1=-2\left(x+2\right)+1`

`y=-2x-3`