Question

The midpoint of segment AB has the coordinates M(-4,2). If the coordinates of endpoint A are (-6, -7), find the coordinates of endpoint B.​

Answer 1

Given:

The midpoint of segment AB has the coordinates M(-4,2).

The coordinates of endpoint A are (-6, -7).

To find:

The coordinates of B.

Solution:

Let the coordinates of point B are (a,b).

Formula for midpoint:

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

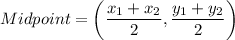
The midpoint of segment AB has the coordinates M(-4,2), so by using the above formula we get

`M=\left((-6+a)/(2),(-7+b)/(2)\right)`

`(-4,2)=\left((-6+a)/(2),(-7+b)/(2)\right)`

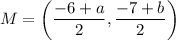
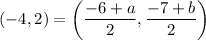
On comparing both sides, we get

`(-6+a)/(2)=-4`

`-6+a=-8`

`a=-8+6`

`a=-2`

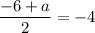
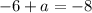
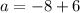
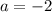
And,

`(-7+b)/(2)=2`

`-7+b=4`

`b=4+7`

`b=11`

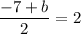
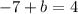
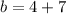
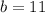
Therefore, the coordinates of point B are (-2,11).