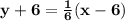Question

What is an equation of the line that passes through the points (6, -6) and (-6, -8)

Answer 1

An equation of the line that passes through the points (6, -6) and (-6, -8) is
`\mathbf{y+6= (1)/(6)(x-6)}`

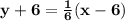
Explanation:

We need to write an equation of the line that passes through the points (6, -6) and (-6, -8)

We would use point slope formula:
`y-y_1=m(x-x_1)`

where
`x_1=6, y_1=-6 \ and \ m \ is \ slope`

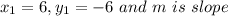
Finding slope using formula:
`Slope=(y_2-y_1)/(x_2-x_1)\\`

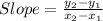
We have
`x_1=6, y_1=-6, x_2=-6, y_2=-8`

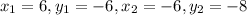
Putting values and finding slope

`Slope=(y_2-y_1)/(x_2-x_1)\\\\Slope=(-8-(-6))/(-6-6)\\Slope=(-8+6)/(-12)\\Slope=(-2)/(-12)\\Slope=(1)/(6)`

So, slope = 1/6

The required equation having
`x_1=6, y_1=-6 \ and \ m =(1)/(6)`

`y-(-6)=(1)/(6)(x-6)\\y+6= (1)/(6)(x-6)`

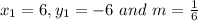
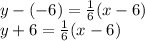
An equation of the line that passes through the points (6, -6) and (-6, -8) is
`\mathbf{y+6= (1)/(6)(x-6)}`