Answer:
Option B. 44 is the correct answer
Step-by-step explanation:
Let l be the number of large pizzas and s be the number of small pizzas
Then according to the given statement the equations will be:

From equation 1

Putting in equation 2

Putting s=72 in equation 1
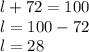
How many more small pizzas means we have to find s-l
So,
s-l = 72-28 = 44
Hence,
Option B. 44 is the correct answer