Question

How do you do these questions?

Answer 1

I'll do the first problem to get you started.

Part (a)

We have a separable equation. Get the y term to the left side and then integrate to get

`(dy)/(dt) = ky^(1+c)\\\\(dy)/(y^(1+c)) = kdt\\\\\displaystyle \int(dy)/(y^(1+c)) = \int kdt\\\\\displaystyle \int y^(-(1+c))dy = \int kdt\\\\\displaystyle -(1)/(c)y^(-c) = kt+D\\\\\displaystyle -(1)/(c*y^(c)) = kt+D\\\\`

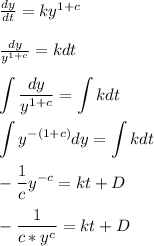
I'm using D as the integration constant rather than C since lowercase letter c was already taken.

Let's use initial condition that
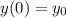`y(0) = y_0`. This means we'll plug in t = 0 and
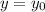`y = y_0`. After doing so, solve for D

`\displaystyle -(1)/(c*y^(c)) = kt+D\\\\\displaystyle -(1)/(c*(y_0)^(c)) = k*0+D\\\\\displaystyle D = -(1)/(c*(y_0)^(c))\\\\`

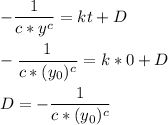
Let's plug that in and isolate y

`\diplaystyle -(1)/(c)y^(-c) = kt+D\\\\\\\diplaystyle -(1)/(c)y^(-c) = kt-(1)/(c*(y_0)^(c))\\\\\\\diplaystyle y^(-c) = -ckt+(1)/((y_0)^(c))\\\\\\\diplaystyle y^(-c) = (1-c*(y_0)^(c)kt)/((y_0)^(c))\\\\\\\diplaystyle (1)/(y^(c)) = (1-c*(y_0)^(c)kt)/((y_0)^(c))\\\\\\\diplaystyle y^(c) = ((y_0)^(c))/(1-c*(y_0)^(c)kt)\\\\\\\diplaystyle y = \left(((y_0)^(c))/(1-c*(y_0)^(c)kt)\right)^(1/c)\\\\\\\diplaystyle y = (y_0)/(\left(1-c*(y_0)^(c)kt\right)^(1/c))\\\\\\`

-------------------------

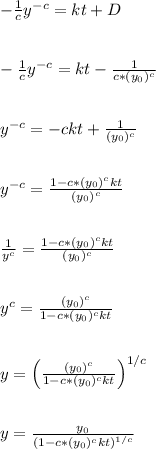
We end up with
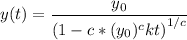`\displaystyle y(t) = (y_0)/(\left(1-c*(y_0)^(c)kt\right)^(1/c))\\\\` as our final solution. There are likely other forms to express this equation.

========================================================

Part (b)

We want y(t) to approach positive infinity.

Based on the solution in part (a), this will happen when the denominator approaches 0 from the left.

So
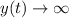`y(t) \to \infty` as
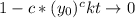`1-c*(y_0)^(c)kt \to 0` in which we can effectively "solve" for t showing that
`t \to (1)/(c*(y_0)^(c)k)`

If we define
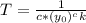`T = (1)/(c*(y_0)^(c)k)` , then approaching T from the left side will have y(t) approach positive infinity.

This uppercase T value is doomsday. This the time value lowercase t approaches from the left when the population y(t) explodes to positive infinity.

Effectively t = T is the vertical asymptote.

========================================================

Part (c)

We're told that the initial condition is y(0) = 5 since at time 0, we have 5 rabbits. This means
`y_0 = 5`

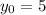
Another fact we know is that y(3) = 35 because after three months, there are 35 rabbits.

Lastly, we know that c = 0.01 since the exponent of dy/dt = ky^(1.01) is 1.01; so we solve 1+c = 1.01 to get c = 0.01

We'll use y(3) = 35, c = 0.01 and
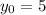`y_0 = 5` to solve for k

Doing so leads to the following:

`\displaystyle y(t) = (y_0)/(\left(1-c*(y_0)^(c)kt\right)^(1/c))\\\\\\\displaystyle y(3) = (5)/(\left(1-0.01*(5)^(0.01)k*3\right)^(1/0.01))\\\\\\\displaystyle 35 \approx (5)/(\left(1-0.0304867k\right)^(100))\\\\\\\displaystyle 35\left(1-0.0304867k\right)^(100) \approx 5\\\\\\\displaystyle \left(1-0.0304867k\right)^(100) \approx (1)/(7)\\\\\\`

`\displaystyle \left(1-0.0304867k\right)^(100) \approx 7^(-1)\\\\\\\displaystyle 1-0.0304867k \approx \left(7^(-1)\right)^(1/100)\\\\\\\displaystyle 1-0.0304867k \approx 7^(-0.01)\\\\\\\displaystyle k \approx (7^(-0.01)-1)/(-0.0304867)\\\\\\\displaystyle k \approx 0.63211155281122\\\\\\\displaystyle k \approx 0.632112\\\\\\`

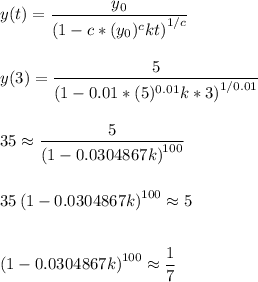
We can now compute the doomsday time value

`T = (1)/(c*(y_0)^c*k)\\\\\\T \approx (1)/(0.01*(5)^(0.01)*0.632112)\\\\\\T \approx (1)/(0.00642367758836)\\\\\\T \approx 155.674064621806\\\\\\T \approx 155.67\\\\\\`

The answer is approximately 155.67 months