I'll do the first problem to get you started.
Part (a)
We have a separable equation. Get the y term to the left side and then integrate to get
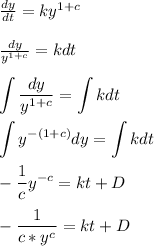
I'm using D as the integration constant rather than C since lowercase letter c was already taken.
Let's use initial condition that
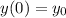 . This means we'll plug in t = 0 and
. This means we'll plug in t = 0 and
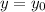 . After doing so, solve for D
. After doing so, solve for D
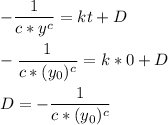
Let's plug that in and isolate y
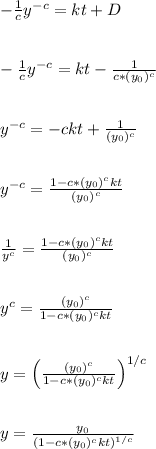
-------------------------
We end up with
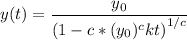 as our final solution. There are likely other forms to express this equation.
as our final solution. There are likely other forms to express this equation.
========================================================
Part (b)
We want y(t) to approach positive infinity.
Based on the solution in part (a), this will happen when the denominator approaches 0 from the left.
So
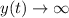 as
as
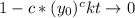 in which we can effectively "solve" for t showing that
in which we can effectively "solve" for t showing that
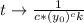
If we define
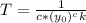 , then approaching T from the left side will have y(t) approach positive infinity.
, then approaching T from the left side will have y(t) approach positive infinity.
This uppercase T value is doomsday. This the time value lowercase t approaches from the left when the population y(t) explodes to positive infinity.
Effectively t = T is the vertical asymptote.
========================================================
Part (c)
We're told that the initial condition is y(0) = 5 since at time 0, we have 5 rabbits. This means
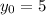
Another fact we know is that y(3) = 35 because after three months, there are 35 rabbits.
Lastly, we know that c = 0.01 since the exponent of dy/dt = ky^(1.01) is 1.01; so we solve 1+c = 1.01 to get c = 0.01
We'll use y(3) = 35, c = 0.01 and
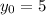 to solve for k
to solve for k
Doing so leads to the following:
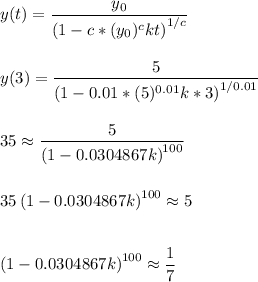

We can now compute the doomsday time value

The answer is approximately 155.67 months