Answer:
Length =
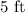
Breadth =
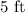
Explanation:
Let
 be the length of the garden
be the length of the garden
and
 be the width of the garden
be the width of the garden
From the details of the cost in the question we get
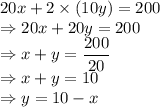
Now area of the garden is
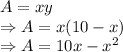
Differentiating with respect to x we get
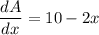
Equating with 0
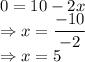
Double derivative of the area is
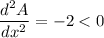
So, area is maximum at

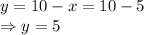
So, the length and breadth of the rectangle is
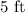 .
.