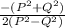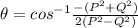Answer:
See below ~
Step-by-step explanation:
Here, let's apply the resultant vector formula :
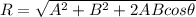
Part (i) :
√3P² + Q² = √(P + Q)² + (P - Q)² + 2(P + Q)(P - Q)cosθ
3P² + Q² = P² + Q² + 2PQ + P² + Q² - 2PQ + 2(P² - Q²)cosθ
2(P² - Q²)cosθ = P² - Q²
cosθ = 1/2
θ = π/3 or 60°
Part (ii) :
√2(P² + Q²) = √(P + Q)² + (P - Q)² + 2(P + Q)(P - Q)cosθ
2(P² + Q²) = P² + Q² + 2PQ + P² + Q² - 2PQ + 2(P² - Q²)cosθ
2(P² - Q²)cosθ = 0
cosθ = 0
θ = π/2 or 90°
Part (iii) :
√P² + Q² = √(P + Q)² + (P - Q)² + 2(P + Q)(P - Q)cosθ
P² + Q² = P² + Q² + 2PQ + P² + Q² - 2PQ + 2(P² - Q²)cosθ
2(P² - Q²)cosθ = -P² - Q²
cosθ =