Question

A small block of mass m1 = 0.4 kg is placed on a long slab of mass m2 = 2.8 kg. Initially, the slab is stationary and the block moves at a speed of vo = 3 m/s. The coefficient of kinetic friction between the block and the slab is 0.15 and there is no friction between the slab and the surface on which it moves.

Determine the speed v1.

Determine the distance traveled by the slab before it reaches the speed v1.

Answer 1

v₁ = 0.375 m / s , x = 0.335 m

Step-by-step explanation:

Let's analyze this interesting exercise, the block moves and has a friction force with the tile, we assume that the speed of the block is constant, so the friction force opposes the block movement. For the only force that acts (action and reaction) this friction force exerted by the block that is in the direction of movement of the tile.

We can also see that the isolated system formed by the block and the tile will reach a stable speed where friction cannot give the system more energy, this speed can be found by treating the system with the conservation of linear momentum.

initial moment. Right at the start of the movement

p₀ = m v₀ + 0

final moment. Just when it comes to equilibrium

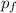`p_(f)` = (m + M) v₁

how the forces are internal

p₀ =p_{f}

m v₀ = (m + M) v₁

v₁ = m /m+M v₀

let's calculate

v₁ = 0.4 /(0.4 + 2.8) 3

v₁ = 0.375 m / s

Let's apply Newton's second law to the Block, to find the friction force

Y axis

N - W = 0

N = W

N = m g

where m is the mass of the block

the friction force has the formula

fr = μ N

fr = μ m g

We apply Newton's second law to slab

X axis

fr = M a

where M is the mass of the slab

μ m g = M a

a = μ g m / M

let's calculate

a = 0.15 9.8 0.4 / 2.8

a = 0.21 m / s²

With kinematics we can find the position

v²= v₀²+2 a x

as the slab is initially at rest, its initial velocity is zero

v² = 2 a x

x = v2 / 2a

let's calculate

x = 0.375²/2 0.21

x = 0.335 m