Question

15.0 moles of gas are in a 8.00 L tank at 22.3 ∘C∘C . Calculate the difference in pressure between methane and an ideal gas under these conditions. The van der Waals constants for methane are a=2.300L2⋅atm/mol2 a=2.300L2⋅atm/mol2 and b=0.0430L/molb=0.0430L/mol.

Answer 1

`\Delta P=4.10atm`

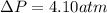
Step-by-step explanation:

Hello!

In this case, since the ideal gas equation is used under the assumption of no interaction between molecules and perfectly sphere-shaped molecules but the van der Waals equation actually includes those effects, we can compute each pressure as shown below, considering the temperature in kelvins (22.3+273.15=295.45K):

`P^(ideal)=(nRT)/(V)=(15.0mol*0.08206(atm*L)/(mol*K)*295.45K)/(8.00L)=45.5atm`

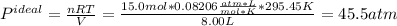
Next, since the VdW equation requires the molar volume, we proceed as shown below:

`v=(8.00L)/(15.0mol)=0.533(L)/(mol)`

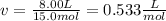
Now, we use its definition:

`P^(VdW)=(RT)/(v-b) -(a)/(v^2)`

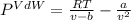
Thus, by plugging in we obtain:

`P^(VdW)=(0.08206(atm*L)/(mol*K)*295.45K)/(0.533mol/L-0.0430L/mol) -(2.300L^2*atm/mol^2)/((0.533L/mol)^2)\\\\P^(VdW)=49.44atm-8.09atm\\\\P^(VdW)=41.4atm`

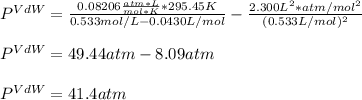
Thus, the pressure difference is:

`\Delta P=45.5atm-41.4atm\\\\\Delta P=4.10atm`

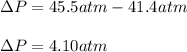
Best regards!