Answer:
The total amount of money Mandy spent is £34.05
Explanation:
1. General Process:
The total amount of money that Mandy spent is the sum (add together) of the money value of all the items she bought. This could be thought of as adding the money-value of each of the individual items, but it can be simplified by grouping common items together and making a subtotal for each category (by "category," I mean the "entire group of all 36 pens", for example), before summing the subtotals of each of the categories.
The total amount of money spent = cost of all pens + cost of all pencils + cost of all rulers + cost of all pencil cases.
2. Watch out for non-common units:
One common challenge with adding is that only numbers with the same units can be added together:
For instance, £1 + £2 = £3. Differently, £1 + 2cats can't really be combined because "£" and "cats" are different units.
In this problem, some of the prices are listed in £, whereas others are listed in p. Values will need to be converted to a common unit in order to sum properly.
For proper unit conversions, we will need to change the numbers for each quantity without changing the actual value it represents. For instance, when one converts £1.50 to pence, it isn't 1.50p. The number must change along with the unit in order for the new quantity to be equal value. £1.50 is 150p. Despite that 1.50 and 150 are two different numbers, both the quantities (with correct units) represent the same amount of money.
3. Find appropriate unit ratios for unit conversions:
Perhaps the most common way to convert units is by using known relationships between units (two quantities that are equal), and forming special ratios (a quotient, or division, of two quantities) called a "unit ratio". A "unit ratio" is a ratio formed from two equal quantities. When two equal quantities are divided, the result (quotient) is 1. The importance of having a unit ratio for converting units is that multiplying by 1, the multiplicative identity, does not change the value that the quantity represents (although the number without units may change, the number with the new units will still represent the same quantity, just in the new units).
Known relationships
There are several relationships given in the problem relating a number of items with a cost of money.
4 pens = 75p which gives the unit ratios
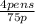 and
and
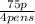
12 pencils = 42p which gives the unit ratios
 and
and
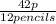
6 rulers = £1.10 which gives the unit ratios
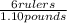 and
and

1 pencil case = 54p which gives the unit ratios
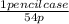 and
and
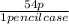
Also, external to this individual problem, it is known that 100p = £1.00 which gives the unit ratios
 and
and
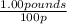
All of the above ratios are unit ratios (equal to 1 for this situation), which will allow us to convert between units for this problem.
4. Finding Subtotals:
To find each subtotal, multiply the number of objects times the unit ratio of cost per object. This will convert from units of "objects" to an equivalent value measured in money. To choose which unit ratios to use, pick a unit ratio with the old unit (the unit we're converting away from) in the denominator (bottom of the fraction) of the unit ratio, and the new unit (the new unit we're trying to obtain) in the numerator (top of the fraction).
For the pens subtotal:
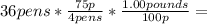 £6.75
£6.75
The units of "p" from the numerator of the second factor cancel with the matching units of "p" in the denominator of the third factor. Similarly, the units of "pens" from the first factor (which could be thought of as a fraction with a denominator of "1" with no denominator units) cancel with the matching units of "pens" in the denominator of the second factor. After these unit cancellations, the only remaining units are pounds or £.
To calculate the number itself, multiply each of the numerators together, and divide by each of the denominators.
For the pencils subtotal:
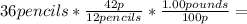 £1.26
£1.26
For the rulers subtotal:
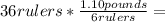 £6.60
£6.60
For the pencil cases subtotal:
 £19.44
£19.44
5. Find final total
Returning to the original idea that the total amount of money spent is simply the sum of the cost of all of the items:
The total amount of money spent = cost of all pens + cost of all pencils + cost of all rulers + cost of all pencil cases.
The total amount of money spent = £6.75 + £1.26 + £6.60 + £19.44
Simply summing the values above, the total amount of money spent by Mandy is £34.05