Question

1. A ball is thrown straight up.if the launch velocity is 15 m/s, at what velocity will the ball return to the thrower's hand?

2. A boat moves across a river going 18 m/s. At the same time there is a current flowing at a right angle to the boat at 6 m/s. What is the resulting velocity of the boat?​

Answer 1

1) The velocity of the ball return to the thrower's hand is -15 meters per second.

2) The resulting velocity of the boat is
`\vec v_(B) = 6\,\hat{i}+18\,\hat{j}\,\left[(m)/(s) \right]`.

Step-by-step explanation:

1) Let suppose that ball experiments a free fall, that is an uniform accelerated motion, in which effects from gravity and Earth's rotation can be neglected. The velocity of the ball is represented by the following equations of motion:

Position

`v_(o)\cdot t -(1)/(2)\cdot g\cdot t^(2) = 0`

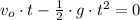
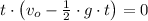`t\cdot \left(v_(o)-(1)/(2)\cdot g\cdot t \right) = 0` (1)

Velocity

`v = v_(o)-g\cdot t` (2)

Where:

`t` - Time, measured in seconds.

`g` - Gravitational acceleration, measured in meters per square second.

`v_(o)` - Initial velocity of the ball, measured in meters per second.

`v` - Final velocity of the ball, measured in meters per second.

From (1), we get the time when the ball returns to the thrower's hand:

`v_(o)-(1)/(2)\cdot g\cdot t = 0`

`t = (2\cdot v_(o))/(g)`

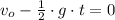
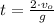
And then we apply this result in (2):

`v = v_(o)-g\cdot \left((2\cdot v_(o))/(g) \right)`

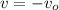`v = -v_(o)` (3)

Then, the velocity of the ball return to the thrower's hand is -15 meters per second.

2) The resulting velocity of the boat (
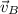`\vec v_(B)`) is represented by the vectorial sum of the velocity of the boat relative to the river (
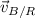`\vec v_(B/R)`) and the velocity of the river (
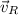`\vec v_(R)`), both measured in meters per second, that is:

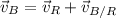`\vec v_(B) = \vec v_(R)+\vec {v}_(B/R)` (4)

If we know that
`\vec v_(R) = 6\,\hat{i}\,\left[(m)/(s) \right]` and
`\vec v_(B/R) = 18\,\hat{j}\,\left[(m)/(s) \right]`, then the resulting velocity of the boat is:

`\vec v_(B) = 6\,\hat{i}+18\,\hat{j}\,\left[(m)/(s) \right]`

The resulting velocity of the boat is
`\vec v_(B) = 6\,\hat{i}+18\,\hat{j}\,\left[(m)/(s) \right]`.