Answer:
a. 11.29 s b. 94.72 m/s at -39.8° c. 821.57 m
Step-by-step explanation:
a. Using y - y₀ = ut - 1/2gt² where u = vertical component of velocity = v₀sinθ where v₀ = 88.3 m/s and θ = 34.5°, y₀ = + 60 m and y = water surface = 0 m, g = 9.8 m/s² and t = time it takes the cannon to reach the water surface.
So y - y₀ = ut - 1/2gt²
y - y₀ = (v₀sinθ)t - 1/2gt²
substituting the values of the variables into the equation, we have
0 - 60 = (88.3 m/s × sin34.5°)t - 1/2 × 9.8 m/s²× t²
- 60 = 50t - 4.9t²
So, 4.9t² - 50t - 60 = 0
Using the quadratic formula to find t,
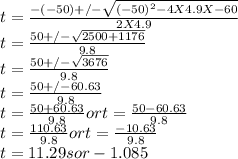
Since t cannot be negative, t = 11.29 s
b. We first need to find the impact vertical velocity component. Using
v = u - gt where u = initial vertical velocity component = v₀sinθ and t = 11.29 s and g = 9.8 m/s². So,
v = v₀sinθ - gt
= 88.3 m/s × sin34.5° - 9.8 m/s² × 11.29 s
= 50.01 m/s - 110.64 m/s
= -60.63 m/s
Since the horizontal velocity is constant u' = v₀cosθ = 88.3 m/s × cos34.5° = 72.77 m/s.
The impact velocity is thus the resultant of the horizontal velocity and final impact velocity. So, V = √(v² + u'²)
= √((-60.63 m/s)² + (72.77 m/s)²)
= √((3676 m²/s² + 5295.48 m²/s²)
= √(8971.48 m²/s²
= 94.72 m/s
The angle θ = tan⁻¹(v/u') = tan⁻¹(-60.63 m/s ÷ 72.77 m/s) = tan⁻¹(-0.8332) = -39.8°
So the impact velocity is 94.72 m/s at -39.8°
c. The horizontal distance out from the base of the cliff that the ball strikes the water is the range, R = u't = 72.77 m/s × 11.29 s = 821.57 m