Question

An astronaut on the moon throws a baseball upward. The astronaut is 6 ft 6 in tall, and the initial velocity of the ball is 40 ft per sec. The heights of the ball in feet is given by the equation

S = -2.7t^2+40t+6.5, where t is the number of seconds after the ball was thrown.

After how many seconds is the ball 18 ft above the moon's surface?

Answer 1

t = 0.293 s and 14.52 s

Explanation:

The heights of the ball in feet is given by the equation as follows :

`S = -2.7t^2+40t+6.5`

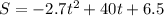
Where t is the number of seconds after the ball was thrown.

We need to find is the ball 18 ft above the moon's surface.

Put S = 18 ft

`-2.7t^2+40t+6.5=18\\\\-2.7t^2+40t=18-6.5\\\\-2.7t^2+40t-11.5=0`

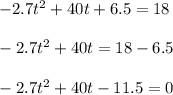
It is a quadratic equation. Its solution is given by :

`t=\frac{-40+\sqrt{40^(2\ )-4\left(-2.7\right)\left(-11.5\right)}}{2\left(-2.7\right)},\frac{-40-\sqrt{40^(2\ )-4\left(-2.7\right)\left(-11.5\right)}}{2\left(-2.7\right)}\\\\t=0.293\ s,14.52\ s`

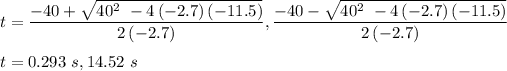
So, the ball is at first 0.293 s and then 14.52 s above the Moon's surface.