Answer:

Explanation:
Density can be found by dividing the mass by the volume.
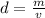
The mass of the block of cheese is 140 grams and the volume is 187 cubic centimeters.

Substitute the values into the formula.
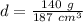
Divide.
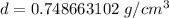
Round to the hundredth place (2 decimal places).
The 8 in the thousandth place tells us to round the 4 to a 5.
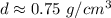
The density is about 0.75 grams per cubic centimeters.