Answer:
Length of sides of triangle are: AB = 15.13, BC = 12.72, AC = 9.21
Explanation:
We need to find the length of sides of the triangle whose vertices are A (7,4), B (-8, 6) C(1, -3).
We have three sides of triangle AB, BC and AC
The length of side can be calculated using distance formula:
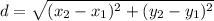
Now finding lengths of sides AB, BC and AC
i) Length of side AB
We have A (7,4), B (-8, 6)
and
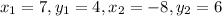
Putting values in formula and finding length

So, Length of side AB is 15.13
ii) Length of side BC
We have B (-8, 6) and C(1, -3)
and

Putting values in formula and finding length

So, Length of side BC is 12.72
iii) Length of side AC
We have A (7,4)and C(1, -3)
and
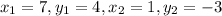
Putting values in formula and finding length
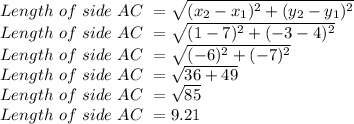
So, Length of side AC is 9.21
So, length of sides of triangle are: AB = 15.13, BC = 12.72, AC = 9.21