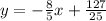Question

Find equation of straight line which

divides the line joining the points P(-1, -4) and Q (7, 1) in the ratio of 3:2 and perpendicular to it.



​

Answer 1

The required equation is:
`y = -(8)/(5)x+(127)/(25)`

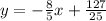
Explanation:

The slope-intercept form of a line is given by:

`y = mx+b`

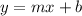
For writing equation of a line, slope and a point is needed from which the line passes.

In order to find the slope of line perpendicular to PQ, we have to find slope of PQ first.

Slope is denoted by m and given by the formula

`m = (y_2-y_1)/(x_2-x_1)`

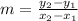
Given points are:

P(-1, -4) and Q (7, 1)

Putting the values

`m = (1-(-4))/(7-(-1))\\m = (1+4)/(7+1) = (5)/(8)`

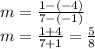
The product of slope of two pependicular lines is -1

Let m1 be the slope of line perpendicular to PQ

`m.m_1 = -1\\(5)/(8).m_1 = -1\\m_1 = (8)/(5) * -1\\m_1 = -(8)/(5)`

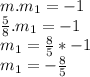
Now for the point, we have to find the point that divides PQ in ratio 3:2

The formula is:

`(x,y) = ((nx_1+mx_2)/(m+n) , (ny_1+my_2)/(m+n))\\`

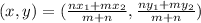
Here

m = 3

n= 2

Putting the values

`(x,y) = (((2)(-1)+(3)(7))/(3+2) , ((2)(-4)+(3)(1))/(3+2))\\= ((-2+21)/(5) , (-8+3)/(5))\\=((19)/(5) , (-5)/(5))\\=((19)/(5) , -1)`

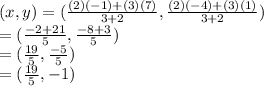
So we have to write equation of a line with slope -8/5 and passing through point (19/5, -1)

Putting the values in slope-intercept form

`y = -(8)/(5)x +b`

Putting the point in the equation

`-1 = -(8)/(5) ((19)/(5)) + b\\-1 = -(152)/(25) + b\\b = -1+(152)/(25)\\b = (-25+152)/(25)\\b = (127)/(25)`

Putting the value of b

`y = -(8)/(5)x+(127)/(25)`

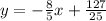
Hence,

The required equation is:
`y = -(8)/(5)x+(127)/(25)`