Question

A toy train engine is rolling freely at a constant speed on a level piece of track. The train engine

collides with a stationary truck, and joins with it. Before the collision the train engine is travelling at
0.30 m/s, and has a mass of 700g. If the stationary truck has as mass of 400g. calculate the speed
of the joined engine and truck immediately after the collision.
(PLEASE answer with working).
​

Answer 1

v₃ = 0.19 [m/s]

Step-by-step explanation:

To solve this problem we must use the principle of conservation of the linear momentum, which is defined as the momentum before the collision is equal to the momentum after the collision.

ΣPbefore = ΣPafter

`P=m*v`

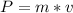
P = momentum [kg*m/s]

m = mass [kg]

v = velocity [m/s]

Let's imagine that the toy train moves to the right, this movement is taken as positive.

`(m_(1)*v_(1))+(m_(2)*v_(2))= (m_(1)+m_(2))*v_(3)`

where:

m₁ = mass = 700 [g] = 0.7 [kg]

v₁ = velocity = 0.3 [m/s]

m2 = mass = 400 [g] = 0.4 [kg]

v₂ = 0 (stationary truck, there is no movement)

v₃ = final velocity of the joined engine and truck.

Now replacing:

`(0.7*0.3)+(0.4*0)= (0.7+0.4)*v_(3)\\0.21 = 1.1*v_(3)\\v_(3)= 0.19 [m/s]`