Question

Solve for x.

a) 9
`9^(3x+4)` =
`27^(4x+3)`
b)
`4^(3x)` =
`2^(x+1)`

(include steps pleez)

Answer 1

Question a)

`9^(3x+4)=27^(4x+3)`

`x=-0.166`

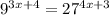
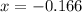
Question b)

`4^(3x)=2^(x+1)`

`x=0.2`

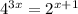
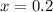
Explanation:

Question a)

Given the expression

`9^(3x+4)=27^(4x+3)`

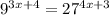
Taking log on both sides

`log\left(9^(3x+4)\right)=log\left(27^(4x+3)\right)`

`\left(3x+4\right)\cdot \left(log\left(9\right)\right)\:=\left(4x+3\right)\cdot \left(log\left(27\right)\right)`

`3x+4=\left((log\left(27\right))/(log\left(9\right))\right)\cdot \left(4x+3\right)`

`3x+4=1.5* \left(4x+3\right)`

`3x+4=6x+4.5`

`3x=6x+0.5`

`(-3x)/(-3)=(0.5)/(-3)`

`x=-0.166`

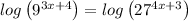
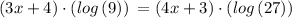
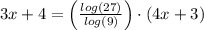
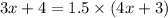
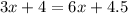
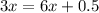
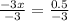
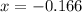
Therefore, the value of x:

`x=-0.166`

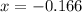
Question b)

Similarly, we can solve the 'b' expression

Given the expression

`4^(3x)=2^(x+1)`

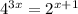
Taking log on both sides

`log\left(4^(3x)\right)=log\left(2^(x+1)\right)`

`3x\cdot \left(log\left(4\right)\right)=\left(x+1\right)\cdot \left(log\left(2\right)\right)`

`3x=\left((log\left(2\right))/(log\left(4\right))\right)\cdot \left(x+1\right)`

`3x=0.5* \left(x+1\right)`

`3x=0.5x+0.5`

`2.5x=0.5`

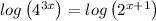
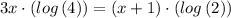
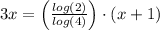
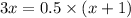
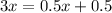
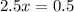
Divide both sides by 2.5

`(2.5x)/(2.5)=(0.5)/(2.5)`

`x=0.2`

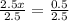
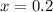
Therefore, the value of x = 0.2