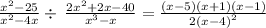Answer:
The factors for the numerator [n] and denominator [d] after reducing will be:
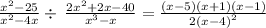
Explanation:
Given the expression
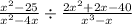
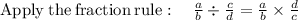
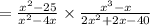
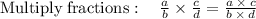
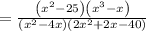
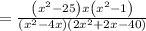
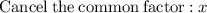
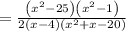
∵ As factor
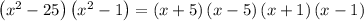
so the expression becomes
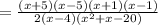
∵ As factor
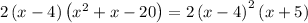
so the expression becomes
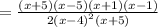
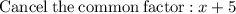
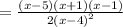
Therefore, the factors for the numerator [n] and denominator [d] after reducing will be: