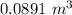Answer:
The capacity of the cistern is
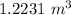
The volume of iron used is
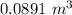
Explanation:
Volume
The volume of a rectangular box of dimensions x,y,z is given by:
V = x.y.z
The external dimensions of the rectangular cistern are 1.35 m, 1.08 m, and 0.90 m, thus the external volume is:
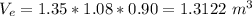
The cistern is made of iron 2.5 cm= 0.025 thick, thus the internal dimensions are:
1.35 - 0.025 = 1.325 m
1.08 - 0.025 = 1.055 m
0.90 - 0.025 = 0.875 m
The internal volume is:
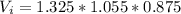
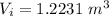
The capacity of the cistern is 1.2231~m^3
The volume of iron used is the difference between the external and the internal volumes:
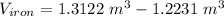
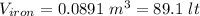
The volume of iron used is