Question

For each equation, determine whether it has no solutions, exactly one solution, or is true for all values of x (and has infinitely many solutions). If an equation has one solution, solve to find the value of x that makes the statement true.

6 x + 8 = 7 x + 13
6 x + 8 = 2 ( 3 x + 4 )
6 x + 8 = 6 x + 13

Answer 1

1. 6x + 8 = 7x + 13
8 = x + 13
x = -5
This has exactly one solution

2. 6x + 8 = 6x + 8
True for all values of x

3. 6x + 8 = 6x + 13
8 = 13
No solution

Answer 2

• Equation 1 has exactly one solution.
• Equation 2 has infinitely many solutions.
• Equation 3 has no solution.

Explanation:

We are given three equations to solve. First, let's solve the equations for x.

Equation 1

`\displaystyle{6x+8=7x+13}\\\\7x + 13 = 6x + 8\\\\x + 13 = 8\\\\\bold{x = -5}`

Therefore, we determined that for the first equation, x = -5. We can check our solution by substituting it back into the original equation.

`\displaystyle{6(-5)+8=7(-5)+13}\\\\-30 + 8 = -35 + 13\\\\-22 = -22 \ \checkmark`

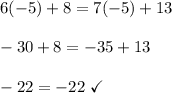
Since we got a true statement, there are no other values of x for which we get a true statement. Let's test this with the opposite value: positive 5.

`6(5)+8=7(5)+13\\\\30 + 8 = 35 + 13\\\\38 = 48 \ \text{X}`

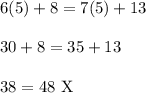
Therefore, for Equation 1, there is exactly one solution.

Equation 2

`6 x + 8 = 2 ( 3 x + 4 )\\\\6x + 8 = 6x + 8\\\\0 + 8 = 8\\\\8 = 8 \ \checkmark`

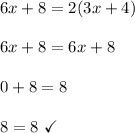
We get a true statement by solving for x (which ends up canceling out of the equation entirely). Therefore, we can check any value in place of x to see if we get a true statement. For this instance, I will use -3.

`6(-3) + 8 = 2 ( 3(-3) + 4 )\\\\-18 + 8 = 2(-9+4)\\\\-18 + 8 = 2(-5)\\\\-18 + 8 = -10\\\\-18 = -18 \ \checkmark`

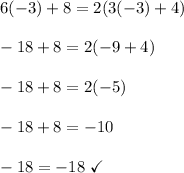
We still get a true statement, so Equation 2 has infinitely many solutions.

Equation 3

`6 x + 8 = 6 x + 13\\\\0 + 8 = 13\\\\8 \\eq 13`

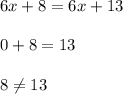
We get a false statement. Therefore, Equation 3 has no solution.