Question

Given: ABC is a right triangle with right angle C. AB= 14 centimeters and mA = 33°

What is AC?
Enter your answer, rounded to the nearest tenth, in the box

Answer 1

AC ≈ 7.6 cm

Explanation:

I've attached a drawing of this problem below as a visual aid.

We know that this is a right triangle (one of the angles is 90°), one of the other angles (mA) is 33°, and the hypotenuse (AB) is 14 cm. We need to calculate the length of one of the other sides. We can use sine, cosine, or tangent.

Remember SOHCAHTOA?

→ soh (Sine = Opposite / Hypotenuse)

→ cah (Cosine = Adjacent / Hypotenuse)

→ toa (Tangent = Opposite / Adjacent)

The side we want to calculate happens to be adjacent to the angle mA (33°). So, we use cosine. We put in the values we know and solve for x, the missing side:

→ sin(33°) =
`(x)/(14)`

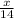
→ x = sin(33°) × 14

→ x ≈ 7.6

The length of AC is 7.6 centimeters.