Question

For a given population of high school seniors, the Scholastic Aptitude Test (SAT) in mathematics has a mean score of 500 with a standard deviation of 100. Assume that the SAT scores are normally distributed. What is the probability that a randomly selected high school senior's score on mathe- matics part of SAT will be

(a) more than 675?
b) between 450 and 675?

Answer 1

To find the probability, we calculate the z-scores for the given scores and find the corresponding areas under the normal curve.

Step-by-step explanation:

To find the probability that a randomly selected high school senior's score on the mathematics part of SAT will be (a) more than 675, we need to calculate the z-score and find the corresponding area under the normal curve. The z-score is calculated as (score - mean) / standard deviation. In this case, the z-score is (675 - 500) / 100 = 1.75. Using a standard normal table or a calculator, we find that the area to the right of 1.75 is approximately 0.0401, which represents the probability that a randomly selected high school senior's score on the mathematics part of SAT will be more than 675.

To find the probability that a randomly selected high school senior's score on the mathematics part of SAT will be (b) between 450 and 675, we can calculate the z-scores for the two scores and find the corresponding areas under the normal curve. The z-score for 450 is (450 - 500) / 100 = -0.5, and the z-score for 675 is (675 - 500) / 100 = 1.75. Using a standard normal table or a calculator, we can find the area to the right of -0.5 and subtract it from the area to the right of 1.75 to get the area between the two scores. This represents the probability that a randomly selected high school senior's score on the mathematics part of SAT will be between 450 and 675.

Answer 2

The probability that a randomly selected high school senior's score on mathematics part of SAT will be

(a) more than 675 is 0.0401

(b)between 450 and 675 is 0.6514

Step-by-step explanation:

Mean of Sat =
`\mu = 500`

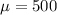
Standard deviation =
`\sigma = 100`

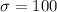
We will use z score over here

What is the probability that a randomly selected high school senior's score on mathe- matics part of SAT will be

(a) more than 675?

P(X>675)

`Z=(x-\mu)/(\sigma)\\Z=(675-500)/(100)`

Z=1.75

P(X>675)=1-P(X<675)=1-0.9599=0.0401

b)between 450 and 675?

P(450<X<675)

At x = 675

`Z=(x-\mu)/(\sigma)\\Z=(675-500)/(100)`

Z=1.75

At x = 450

`Z=(x-\mu)/(\sigma)\\Z=(450-500)/(100)`

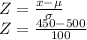
Z=-0.5

P(450<X<675)=0.9599-0.3085=0.6514

Hence the probability that a randomly selected high school senior's score on mathematics part of SAT will be

(a) more than 675 is 0.0401

(b)between 450 and 675 is 0.6514