Question

An oxygen–nitrogen mixture consists of 35 kg of oxygen and 40 kg of nitrogen. This mixture is cooled to 84 K at 0.1 MPa pressure. Determine the mass of the oxygen in the liquid and gaseous phase.

Answer 1

The mass of oxygen in liquid phase = 14.703 kg

The mass of oxygen in the vapor phase = 20.302 kg

Step-by-step explanation:

Given that:

The mass of the oxygen
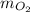`m_(O_2)` = 35 kg

The mass of the nitrogen
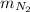`m_(N_2)` = 40 kg

The cooling temperature of the mixture T = 84 K

The cooling pressure of the mixture P = 0.1 MPa

From the equilibrium diagram for te-phase mixture od oxygen-nitrogen as 0.1 MPa graph. The properties of liquid and vapor percentages are obtained.

i.e.

Liquid percentage of
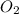`O_2` = 70% = 0.70

Vapor percentage of
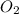`O_2` = 34% = 0.34

The molar mass (mm) of oxygen and nitrogen are 32 g/mol and 28 g/mol respectively

Thus, the number of moles of each component is:

number of moles of oxygen = 35/32

number of moles of oxygen = 1.0938 kmol

number of moles of nitrogen = 40/28

number of moles of nitrogen = 1.4286 kmol

Hence, the total no. of moles in the mixture is:

`N_(total) = 1.0938+1.4286`

`N_(total) = 2.5224 \ kmol`

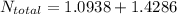
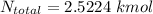
So, the total no of moles in the whole system is:

`N_f + N_g = 2.5224 --- (1)`

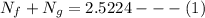
The total number of moles for oxygen in the system is

`0.7 \ N_f + 0.34 \ N_g = 1.0938 --- (2)`

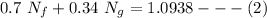
From equation (1), let N_f = 2.5224 - N_g, then replace the value of N_f into equation (2)

∴

0.7(2.5224 - N_g) + 0.34 N_g = 1.0938

1.76568 - 0.7 N_g + 0.34 N_g = 1.0938

1.76568 - 0.36 N_g = 1.0938

1.76568 - 1.0938 = 0.36 N_g

0.67188 = 0.36 N_g

N_g = 0.67188/0.36

N_g = 1.866

From equation (1)

`N_f + N_g = 2.5224`

N_f + 1.866 = 2.5224

N_f = 2.5224 - 1.866

N_f = 0.6564

Thus, the mass of oxygen in the liquid and vapor phases is:

`m_(fO_2) = 0.7 * 0.6564 * 32`

`m_(fO_2) = 14.703 \ kg`

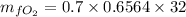
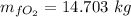
The mass of oxygen in liquid phase = 14.703 kg

`m_(g_O_2) = 0.34 * 1.866 * 32`

`m_(g_O_2) = 20.302 \ kg`

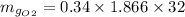
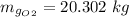
The mass of oxygen in the vapor phase = 20.302 kg