Question

A mass slides from rest down a 45 degree incline that has a coefficient of kinetic friction

equal to 0.2. What is the speed of the mass after it has slid for a total of 2 meters?

Answer 1

The speed of the mass after it has slid for a total of 2 meters is 4.71 m/s.

Step-by-step explanation:

The speed of the mass can be found using Newton second law:

`\Sigma F = ma`

`P_(x) - F_{\mu_(k)} = ma`

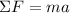
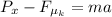
Where Pₓ is the weight force in the horizontal direction and
`F_{\mu_(k)}` is the friction force.

`mgsin(\theta) - \mu_(k)mgcos(\theta) = ma`

`a = g(sin(\theta) - \mu_(k)cos(\theta)) = 9.81 m/s^(2)(sin(45) - 0.2*cos(45)) = 5.55 m/s^(2)`

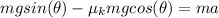
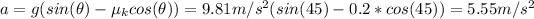
Now, we can find the speed of the mass using the following kinematic equation:

`v_(f)^(2) = v_(0)^(2) + 2ax`

`v_(f) = \sqrt{0 + 2*5.55 m/s^(2)*2 m} = 4.71 m/s`

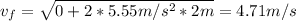
Therefore, the speed of the mass after it has slid for a total of 2 meters is 4.71 m/s.

I hope it helps you!