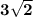Answer:
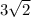
Explanation:
The Magnitude of a Complex Number
A complex number is expressed in rectangular form as:
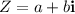
The absolute value or magnitude of Z is calculated as follows:
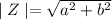
We are given the number
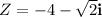
Here: a= -4, b=
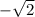
Calculating the absolute value:
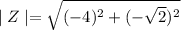
Operating:
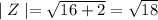
Factoring 18:
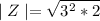
Taking the square root of 3^2:
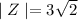
Answer: