Question

A substance with a half life is decaying exponentially. If there are initially 12grams of the substance and after 70 minutes there are 7 grams, after how many minutes will there be 2 grams remaining?

Answer 1

Explanation:

Use the half life formula

`N=N_0e^(kt)` where N is the amount after decay, No is the initial amount, e is Euler's number, k is the decay constant, and t is the time in minutes. For us, the first equation looks like this:

`7=12e^(k(70))` and we will solve that for k and then use that value of k in the second equation to find time.

Begin by dividing 7 by 12 to get

`(7)/(12)=e^(k(70))` Now take the natural log of both sides since the natural log and that e are inverses. The e then disappears:

`ln((7)/(12))=k(70)`

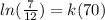
Plug the left side into your calculator and then set it equal to the right side, giving us:

`-.5389965007=70k`

Divide both sides by 70 to get the k value of

k = -.00769995

Now the second equation looks like this:

`2=12e^{(-.00769995)t` where t is our only unknown now that we know k.

Begin by dividing both sides by 12 to get

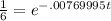`(1)/(6)=e^{-.00769995t` and take the natural log of both sides again to eliminate the e:

`ln((1)/(6))=-.00769995t`

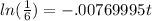
Take care of the left side on your calculator to get

-1.791759469 = -.00769995t and divide both sides by -.00769995 to get

t = 232.697 minutes