Question

You are the manager of a donut shop. Presently, you sell your donuts for $1.00 each and everyday you sell 500 donuts. However, you are wondering if you could make a bit more profit by raising the price slightly. Your marketing research shows that for every $0.05 you raise the price, you will sell 10 less donuts. What price would result in the most revenue?

Answer 1

Answer: $1.75

Solve for:

What price would result in the most revenue?

Explanation:

Let the price of one donut = 1 + 0.05x

Let the # of donuts he can sell = 500 - 10x

Revenue,

`R(x) = (1 + 0.05x)(500 - 10x)`

`R(x) = 500 - 10x + 25x - 0.5x^2`

`R(x) = -10 + 25-0.5(2x)`

`= 15-x\\x=15`

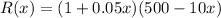
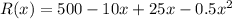
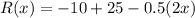
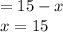
Revenue is maxed when x = 15

When the revenue is maxed,

`Price = 1 + 0.05(15)\\=1 + 0.75\\=1.75`

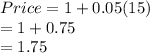
Therefore the best price for this scenario is $1.75