Answer:
The coordinates of the turning point are (2, -9)
Explanation:
The coordinates of the turning points of the quadratic equation
y = ax² + bx + c, are (h, k), where
- h =
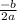
- k is the value of y at x = h
∵ The equation of the curve is y = x² + bx + c
→ By comparing it with the form above
∴ a = 1
∵ The point (0, -5) lies on the curve
→ Substitute x by 0 and y by -5 in the equation to find the value f c
∵ -5 = (0)² + b(0) + c
∴ -5 = 0 + 0 + c
∴ -5 = c
→ Substitute it in the equatin
∴ y = x² + bx - 5
∵ The point (5, 0) lies on the curve
→ Substitute x by 5 and y by 0 in the equation to find the value f c
∵ 0 = (5)² + b(5) - 5
∴ 0 = 25 + 5b - 5
→ Add the like terms in the right side
∴ 0 = 20 + 5b
→ Subtract 5b from bth sides
∵ 0 - 5b = 20 + 5b - 5b
∴ -5b = 20
→ Divide both sides by -5 to find b
∴ b = -4
→ Substitute it in the equatin
∴ y = x² - 4x - 5
∵ a = 1 and b = -4
→ Substitute them in the rule of h above t find it
∵ h =
 =
=
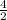
∴ h = 2
→ To find k, substitute x by 2 and y by k
∵ k = (2)² - 4(2) - 5
∴ k = 4 - 8 - 5
∴ k = -9
∴ The cordinates of the turning point are (2, -9)