Question

What is the slope of the line that contains these points?

Answer 1

`\boxed {\boxed {\sf m=7}}`

Explanation:

To find the slope, we can use the slope formula.

`m=(y_2-y_1)/(x_2-x_1)`

where (x₁, y₁) and (x₂, y₂) are points on the line.

We can pick any two points in the chart.

Let's use (-1, 35) and (2,56).

If we use these points, then the variables are:

`x_1=-1 \\y_1=35 \\x_2=2 \\y_2=56`

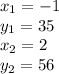
Substitute the values into the formula.

`m=(56-35)/(2--1)`

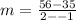
Solve the numerator.

• 56-35=21

`m=(21)/(2--1)`

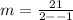
Solve the denominator.

• 2--1= 2+1=3

`m=(21)/(3)`

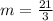
Divide.

`m=7`

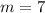
The slope of the line is 7

Answer 2

`m=7`

General Formulas and Concepts:

Pre-Algebra

• Order of Operations: BPEMDAS

Algebra I

• Slope Formula:
  `m=(y_2-y_1)/(x_2-x_1)`

Explanation:

Step 1: Define

Find points from chart.

Point (-7, -7)

Point (-4, 14)

Step 2: Find slope m

1. Substitute:
   `m=(14+7)/(-4+7)`
2. Add:
   `m=(21)/(3)`
3. Divide:
   `m=7`