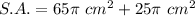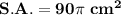2 Answers

Anel · Answer 1 · 2021-01-18T17:25:41+0000

Answer:

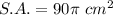
$S.A.=90\pi~cm^2$

Explanation:

Surface Area of a Cone

Given a cone of base area B and slant height L, the surface area can be calculated with the formula:

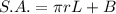
$S.A.=\pi rL +B$

The cone presented in the image has a circular base of radius r=5 cm, thus its base area is:

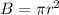
$B=\pi r^2$

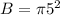
$B=\pi 5^2$

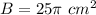
$B=25\pi~cm^2$

The slant height can be calculated as the hypotenuse of a right triangle with legs 5 cm and 12 cm by using Pythatgora's Theorem:

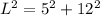
L^2=5^2+12^2

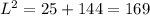
L^2=25+144=169

Taking square roots

L = √(169)

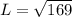
L = 13 cm

The surface area is:

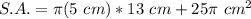
$S.A.=\pi (5~cm)*13~cm +25\pi~cm^2$

Operating:

$S.A.=65\pi~cm^2 +25\pi~cm^2$

$\mathbf{S.A.=90\pi~cm^2}$

Please log in or register to add a comment.