Answer:
8.4 cm
Explanation:
Given that:
A right angled triangle, let
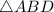 . Right angled at
. Right angled at
 .
.
Altitude AC to the hypotenuse BD.
Length of side BC = 5 cm
Length of side CD = 11 cm
We have to find the value of shorter leg of triangle. i.e. side AB = ?
Using the concept of similarity, we can say the following:

The length of shorter leg of the triangle = 8.4 cm