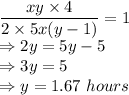Answer:
1.67 hours
Explanation:
Let the original speed of Jonathan =
 units/hr
units/hr
Let the original time taken by Jonathan =
 hours
hours
Let the distance =
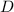 units
units
Formula for distance is given as:
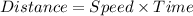
Given that half the distance is covered by original speed.
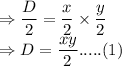
Half the distance is covered by increasing the rate by 25%.
i.e. increased speed:

Hence, Time taken:

Distance traveled is half of the total distance:
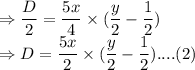
Dividing (1) by (2):