Question

Mr. Moretti is making welcome bags to give to the 18 students in his homeroom on the first day of school he puts m mechanical pencils in each bag he puts twice as many regular pencils in each bag

Answer 1

Mr. Moretti puts (18) mechanical pencils and (36) regular pencils in each welcome bag for a total of (54) pencils in each bag.

Given that Mr. Moretti puts twice as many regular pencils as mechanical pencils in each bag, we can represent the number of regular pencils as (2m) where (m) is the number of mechanical pencils. The total number of pencils in each bag is the sum of the mechanical pencils and regular pencils, i.e., (m + 2m = 3m). Since there are (18) students in his homeroom,
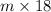`\(m * 18\)` mechanical pencils and
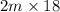`\(2m * 18\)` regular pencils will be needed for all the welcome bags.

Substituting (m = 18) into the expression (3m), we find that each bag contains (18 + 2(18) = 54) pencils in total. Therefore, Mr. Moretti puts (18) mechanical pencils and (36) regular pencils in each welcome bag.

Understanding the relationship between the number of mechanical and regular pencils and applying basic algebraic expressions is key in solving this problem. By defining the number of regular pencils in terms of (m) (the number of mechanical pencils) and recognizing the total as (3m), the calculation becomes straightforward. In the context of creating welcome bags, this mathematical approach ensures an efficient and consistent distribution of pencils for each student in Mr. Moretti's homeroom.

Answer 2

The total number of pencils is 6

Explanation:

According to the given scenario, the computation of the total number of pencils is as follows:

There are 18 students

And let us assume there is m mechanical pencils that put in each bag

also he put twice of the regular pencil

So if he put the 3 mechanical pencil

So, the total number of pencils is

= 3 × 2

= 6

As it twice of the regular pencil

hence, the total number of pencils is 6