Question

Can anyone help me with this plzz?

Answer 1

Answer: 12pi

===========================================================

Step-by-step explanation:

Check out figure 1 in the attached images below. In this figure, I've plotted the function y = 6/(2x-3) on a 2D grid system. The function curve is in blue. Then I've plotted (2,0) and (3,0) on the x axis. Point A is somewhere between those endpoints. Point A is also on the x axis. Directly above A is point B such that B is on the blue function curve.

The distance from A to B is found by subtracting the y values of each point.

The y coordinate of A is y = 0. The y coordinate of B is y = 6/(2x-3)

Therefore, the distance from A to B is 6/(2x-3) units. This will form the radius of each cylindrical slice as figure 2 shows. Note the color coding to help see how the 2D view corresponds to the 3D view. The xy plane has been laid flat on the floor. So we're viewing the function curve at a downward angle now. Each of those gray cylinders combine to form an approximate 3D volume. The more cylinders we have, and the finer the cuts, the more accurate the total volume.

So it comes down to finding the volume of each cylindrical slice and adding up the volumes. This is effectively what integral calculus is all about.

------------------------------------

Since the radius of each cylinder is y = 6/(2x-3), this means r = 6/(2x-3) is plugged into the formula

V = pi*r^2*h

which is the volume of a cylinder formula

The height of each cylinder is delta x, which we'll use dx for short. So this is where the dx comes from in integrals.

This is what the integral will look like

`\displaystyle V = \int_(2)^(3) \pi*\left((6)/(2x-3)\right)^2dx`

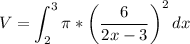
which turns into

`\displaystyle V = 36\pi\int_(2)^(3)(1)/((2x-3)^2)dx`

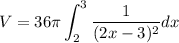
after a bit of algebra. We're able to factor the 36pi out because it's a constant

From here we use u-substitution. Let u = 2x-3

This leads to du/dx = 2 which can be solved to dx = du/2

Since u = 2x-3, the lower endpoint x = 2 leads to

u = 2x-3 = 2*2-3 = 1

and x = 3 leads to

u = 2x-3 = 2*3-3 = 3

So the interval 2 < x < 3 turns into 1 < u < 3

After using u-sub, making the proper replacements, and integrating, we get

`\displaystyle V = 36\pi\int_(2)^(3)(1)/((2x-3)^2)dx\\\\\\\displaystyle V = 36\pi\int_(1)^(3)(1)/(u^2)(du)/(2)\\\\\\\displaystyle V = 36\pi*(1)/(2)\int_(1)^(3)(1)/(u^2)du\\\\\\\displaystyle V = 18\pi\int_(1)^(3)u^(-2)du\\\\\\\displaystyle V = 18\pi\left[-u^(-1)+C\right]_(1)^(3)\\\\\\\displaystyle V = 18\pi\left[-(1)/(u)+C\right]_(1)^(3)\\\\\\`

Let's evaluate that to get the following

`\displaystyle V = 18\pi\left[-(1)/(u)+C\right]_(1)^(3)\\\\\\\displaystyle V = 18\pi\left[\left(-(1)/(3)+C\right)-\left(-(1)/(1)+C\right)\right]\\\\\\\displaystyle V = 18\pi\left(-(1)/(3)+1\right)\\\\\\\displaystyle V = 18\pi\left((2)/(3)\right)\\\\\\\displaystyle V = 12\pi\\\\\\`

So the 3D volume formed by rotating that region (under the curve from x = 2 to x = 3) is exactly 12pi cubic units